Tries

When you type something on your phone, do you ever wonder how it starts showing autocomplete suggestions?

For instance, if you type in ‘ap’ in your phone’s search bar, it might suggest apple, apricot, or any other word that starts with ‘ap’.

How do you think this is implemented? Well, if you were to use an array, you’d have to search the whole array to find all the elements that have ‘ap’ as their prefixes.

listOfItems = ['banana', 'apple', 'cat', 'dog', 'fish', 'chicken', 'meat', 'lentils', 'apron']

Consider the array above. Say we want to find ‘ap’. We’ll have to look at all of the elements in the array to find all the words that start with ‘ap’. 

Now, let’s consider the trie data structure.

 

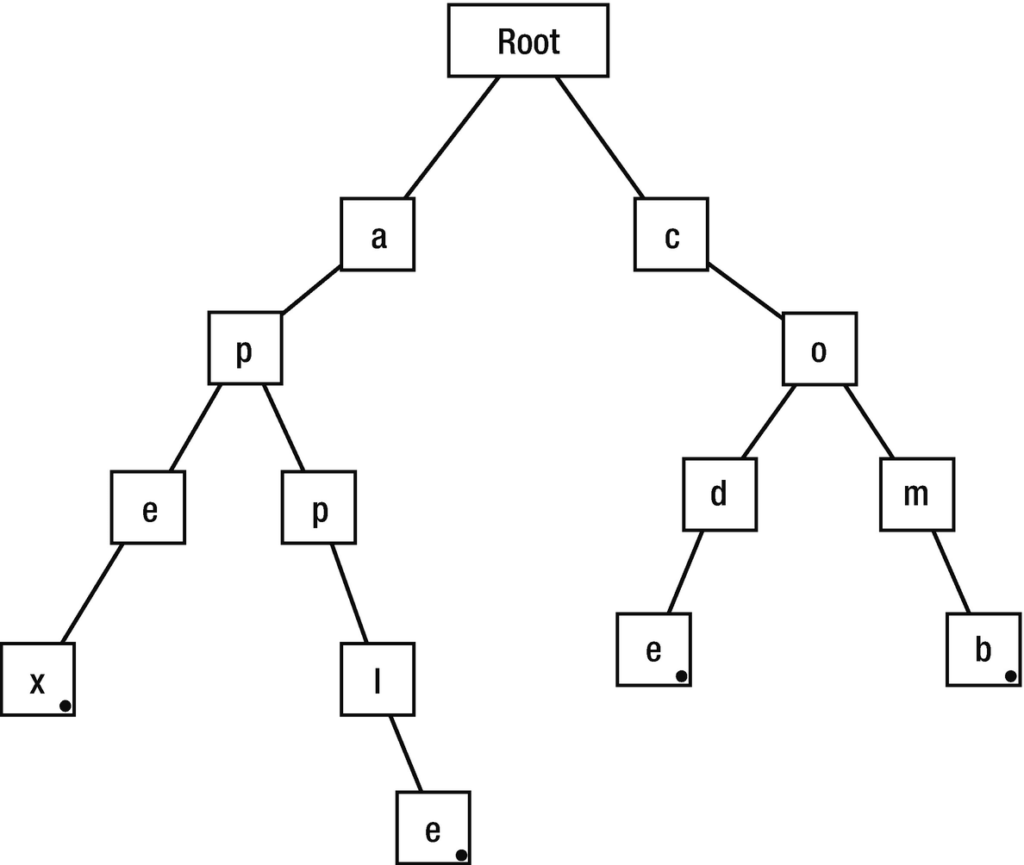
It kind of looks like a tree, doesn’t it? Well, it is one. More specifically, it’s a special kind of tree called a search tree. 

Note how the parent, the root, has no value. It’s just called root. This is because this is just the initial parent node that will help us traverse through the root.

Let’s walk through an example so that we get a better understanding.

This will be our initial root node. Nothing too fancy. However, under the hood, it’s built a little bit differently from a traditional binary tree node.

In a trie’s node, we’ll store the following:

• The node’s character itself – if we’re on a ‘c’ node, our node’s character is ‘c’.
• The children – we have 26 letters in the alphabet, so we’ll have a list of size 26 for each child letter.
• A true or false value – this’ll depend on whether the node represents the end of a word or not.
• A counter – this will show us the count of words that use the current node.

Imporant note: A node’s number of children depends on the possible letters there can be in a string. In this implementation, we’ll assume we’re only working with lowercase alphabet letters. Since there are 26 characters in the alphabet, each node will have 26 children.

Let’s try adding the word ‘comb‘ to the trie. We’ll iterate through the word comb then add each letter to the trie along the way. 

So, let’s first enter the root node. We’ll check if the root node has a child node with ‘c’ as its value. It doesn’t, so it creates one and then travels to that node. 

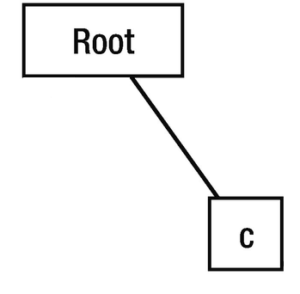
Now, we are at the ‘c’ node. We’ll check if ‘o’ is a child of the ‘c’ node. It isn’t, so it’ll create one and then travel there.

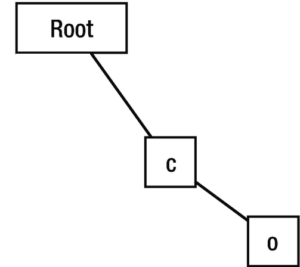
Now, we’re at the ‘o’ node. We’ll check if ‘m’ is a child of the ‘o’ node. It isn’t, so it’ll create an ‘m’ node then travel there. 

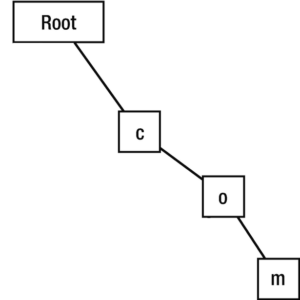
Now, we’re at the ‘m’ node. We’ll check if b is a a child of the ‘m’ node. It isn’t, so it’ll create a ‘b’ node than traverse there.

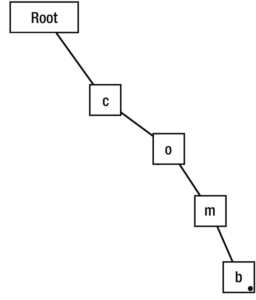
We’ve iterated through the entire word we are trying to add, so we are done traversing through the trie.

Now, all we have to do is modify the last node by letting it know that it’s a word. This’ll be necessary when we search for the word later.

Let’s walk through another example. This time, we’ll add the word ‘code‘. We again iterate through each letter in the word ‘code’.

Do we have a ‘c’ child in our initial root? We do, so let’s travel there and increment its counter by 1. 

Note: We increment the counter of a node that already exists by 1, so that our search is easier when we are looking for words that start with a common prefix. For instance, if we wanted to know the amount of words that have ‘c’ as its prefix, all we have to do is travel to that node and look up its counter. Since the counter is 2, we’ll know that there are two words with ‘c’ as its prefix.

Now, do we have an ‘o’ child in our ‘c’ node? We do, so let’s travel there and also increment its counter by 1.

Now, do we have a ‘d’ child in our ‘o’ node? We don’t, so let’s create one then travel there.

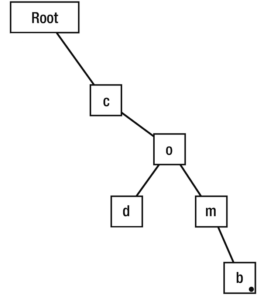
We are now at the ‘d’ node. Does the ‘d’ node have ‘e’ as its child? Nope, so let’s create one then travel there.

We’re now at the ‘e’ node. Now, since we have iterated through the entire word ‘code’, let’s modify this node and let it know that it’s a word. 

Now to really point the strength of this data structure, let’s add two new words that don’t start with a ‘c’.

 

We added the words apex and apple. Now, let’s assume our problem is to find the total number of words that have the prefix ‘co’.

Let’s assume we used an array to solve this problem. 

listOfItems = ['apex', 'apple', 'code', 'comb']

We’d have to traverse through the entire array and check if each individual item started with the prefix ‘co’.

Note: If the array was sorted, we could’ve run a binary search on the array. However, adding and deleting words from a sorted array can be slow. Adding a word takes the same amount of time as searching for a word with a trie.

Now, let’s instead assume we used a trie. 

We visit our root node and check if ‘c’ is a child. It is, so we then check if ‘o’ is a child of ‘c’. It is, so we ask ‘o’ for its counter. Now, its counter is just the amount of words with that prefix. It tells us its counter is 2, and we have our answer.

Notice how searches with an array would require N operations (with N being the size of the array) and how searches with a trie only require M operations (with M being the length of the prefix). 

Arrays require N operations, because the last element could be a word with the prefix specified (as it is in our listOfItems example above).

Trie Node Implementation

So, let’s start implementing the trie node.

class TrieNode:
    def __init__(self, character):
        self.character = character  # Character of the node itself.
        self.isWord = False  # Boolean that determines whether this node is the end of a word.
        self.counter = 1  # Count of how many times this node is used.
        self.children: List[TrieNode or None] = [None] * 26  # 26 possible children for each node.

We’ll store the character itself, a boolean determining whether it’s a word or not, a count of how many times this node is used, and its children.

Trie Implementation

Next, let’s implement the trie.

For this trie implementation, we’ll have the following functions:

• get_index_of_letter(letter) – this will return us a 0-indexed position of the letter in the alphabet. For instance, a would return 0, b would return 1, c would return 2, d would return 3, and so on.
• helper_traverse_trie(target) – this will help us traverse through the trie in search of some target string. If the search comes up positive, it’ll return the last node it visited. If the target couldn’t be found, it’ll return None.
• count(prefix) – this will return the total count of words with the prefix specified.
• is_word(word) – this will return True or False depending on whether the word provided is a word in the trie or not.
• is_prefix(prefix) – this will return True or False depending on whether the prefix exists or not.
• get_words_count() – this will return the total number of words in the trie.
• get_words(prefix) – this will return all the trie’s possible words with the prefix provided.
• get_all_words() – this will return all the words in the trie.
• add(word) – this will add the word given to the trie (if it doesn’t exist).
• delete(word) – this will delete the word from the trie (if it exists).
• delete_words_with_prefix(prefix) – this will delete all the trie’s words with the prefix provided.
• is_empty() – this will return True or False depending on whether the trie has words or not.
• clear() – this will delete all the words from the trie and reset the root node.
• teach(file) – this will read the provided file then add each word from the file to the trie.

Let’s start off by creating the constructor:

class Trie:
    def __init__(self):
        self.root = TrieNode('*')  # Root parent node. The * character doesn't mean anything.
        self.root.counter = 0  # Reset the counter to 0 as no words have been added yet.

Pretty straightforward. We create our root variable and set it equal to our first trie node. We then reset the trie node’s counter to 0 as we have no words in the trie.

Next, let’s implement the index function:

@staticmethod
def get_index_of_letter(letter) -> int:
    """
    Returns the index of the letter from 0 - 25 inclusive depending on alphabetic order.
    :param letter: Letter to check index of.
    :return: Letter's index in the alphabet.
    """
    return ord(letter) - ord('a')

All the nodes in our implementation of the trie have 26 children. To check if a child node exists, we just check the alphabetic index of the children array. For instance, to check if a node has a child that’s the letter ‘b’, we can just check the node’s children array and check its second index.

children = [None, TrieNode, None, None]

In this children array, the second index is a TrieNode, so the child node ‘b’ must exist. If the letter is ‘c’, we check the third index; if the letter is ‘d’, we check the fourth index, and so on and so forth.

Note: Array indices start from 0 instead of 1. So if we want to check the 4th index, we’ll need to check the 3rd index. (Because, it’s 0, 1, 2, 3). 

Next, let’s implement the helper_traverse_trie(target) function.

This’ll traverse through the trie and return the node of the string’s final letter in the trie (if it exists).

def helper_traverse_trie(self, target) -> TrieNode or None:
    """
    Helper function that will traverse through the trie looking for the specified target.
    :param target: Target string to find.
    :return: Final node of the string if it exists, else None.
    """
    node = self.root

    for letter in target:
        index = self.get_index_of_letter(letter)
        if node.children[index]:
            node = node.children[index]
        else:
            return None
    return node

We’ll traverse through each letter in the target as we did in the visual example above. If a child node with the specified letter exists, we’ll traverse there. Then we’ll check if the next letter exists in the next node and repeat this logic until we go through all our letters. Once we’ve gone through all our letters, we’ll return the node we’re at.

If there doesn’t exist a child node at any point, we just return None.

Next, let’s implement the count(prefix) function. 

def count(self, prefix) -> int:
    """
    Returns the count of words with the prefix provided.
    :param prefix: Prefix to be counted.
    :return: Count of words with prefix provided.
    """
    node = self.helper_traverse_trie(target=prefix)

    if node:
        return node.counter
    return 0

We’ll call the helper_traverse_trie() function and check the node that it returned. If that node exists, return its counter; it it doesn’t exist, then return 0 (as this means, no word with this prefix exists).

Next, let’s implement the is_word(word) function. 

def is_word(self, word) -> bool:
    """
    Returns whether or not word provided is a word in the trie.
    :param word: Target string to check if it's a word in the trie.
    :return: Boolean whether it's a word in the trie or not.
    """
    node = self.helper_traverse_trie(target=word)

    if node:
        return node.isWord
    return False

We’ll call the helper_traverse_trie() function and check the node that it returned. If that node exists, we’ll return True if that node is a word and False if it isn’t. If no node is returned, that means there definitely isn’t a word, so return False.

Next, let’s implement the is_prefix() function:

def is_prefix(self, prefix) -> bool:
    """
    Returns whether the prefix exists in the trie or not.
    :param prefix: Prefix to check if exists in the trie.
    :return: Boolean whether prefix exists in the trie or not.
    """
    node = self.helper_traverse_trie(target=prefix)
    return node is not None

We’ll call the helper_traverse_trie() function and check the node that it returned. If the node exists, we’ll return True; if it doesn’t, we’ll return False. 

Next, let’s implement the get_words_count() function.

def get_words_count(self) -> int:
    """
    Returns total number of words in the trie.
    :return: Total number of words in the trie.
    """
    return self.root.counter

This will just return the counter of our root node. We increment or decrement this counter depending on whether we add or delete something from the trie, so this will reflect the total count of words in the trie.

Next, let’s implement the get_words() function.

def get_words(self, prefix) -> List[str]:
    """
    Returns possible words from prefix provided.
    :param prefix: Target prefix for all possible words to have.
    :return: List of all possible words from the trie with the provided prefix.
    """
    node = self.helper_traverse_trie(target=prefix)
    suggestions = []

    if node:
        queue = deque()  # Run BFS to find all possible words sorted in length then alphabetical order.
        queue.append((node, ''))  # Add tuple of node and initial string of '' to queue.

        while queue:
            poppedItem = queue.popleft()
            currentNode = poppedItem[0]
            if currentNode.isWord:
                suggestions.append(prefix + poppedItem[1])
            for child in currentNode.children:
                if child:
                    queue.append((child, poppedItem[1] + child.character))

    return suggestions

Important note: If you don’t know what breadth first search or depth first search is, consider researching them before moving on.

This function is the most complex function we’ll have in the trie. We’ll first get the node with the helper_traverse_trie() function. Then initialize an empty suggestions list.

We then check if the node exists. If it does, then we’ll run a breadth first search with the node. We run breadth first search because we want to sort our suggestions by length then alphabetic order. 

While we’re running the breadth first search, we’ll check if the node we’re at is a word. If it is, then we’ll add the word to the suggestions list.

Once we’ve completed our search, we’ll return our suggestions list.

Next, let’s implement the get_all_words() function:

def get_all_words(self) -> List[str]:
    """
    Returns all words in the trie.
    :return: List of all words present in the trie.
    """
    return self.get_words('')

This function will return a list of all the words we have in the trie. Calling the function get_words() with an empty string as the prefix will do the trick.

Next, let’s implement the add(word) function:

def add(self, word):
    """
    Adds word provided to the trie.
    :param word: Word to add to the trie.
    :return: None
    """
    if not self.is_word(word) and len(word) > 0:  # Check if the word isn't already in the trie.
        node = self.root
        node.counter += 1  # Increment root counter by 1 to point out a new word exists in the trie.

        for letter in word:
            index = self.get_index_of_letter(letter)
            if node.children[index]:
                node = node.children[index]
                node.counter += 1
            else:
                trieNode = TrieNode(letter)
                node.children[index] = trieNode
                node = trieNode

        node.isWord = True

We first check if the word exists in the trie. If it does, we skip as we don’t want any duplicates.

Then, it is the same logic as we discussed visually above. We iterate through each letter in the word. If a node connected to that letter exists, we increment that node’s counter by 1, if it doesn’t, we create a new node in the parent node’s children array. Then, we traverse to the child node and repeat.

Finally, once we’ve gone through all the letters, we modify the node we’re at and modify it to reflect that it’s a word.

Next, let’s implement the delete() function:

def delete(self, word):
    """
    Deletes a word from the trie if it exists.
    :param word: Word to be deleted from the trie.
    :return: None
    """
    if self.is_word(word):  # Make sure the word exists first.
        node = self.root
        node.counter -= 1  # Decrement root counter.
        for letter in word:
            index = self.get_index_of_letter(letter)
            if node.children[index].counter <= 1:
                node.children[index] = None
                return  # If the counter of the index is 1 or less, just set that child to None and we're done.
            else:
                node.children[index].counter -= 1
                node = node.children[index]
        node.isWord = False  # Since, we deleted this word, we set the isWord boolean to be False.

We first search if it’s a word. If it’s not a word in the first place, just return.

However, if it is a word, then travel through each child node and decrement the counter by 1. If the counter then happens to be 0, then just delete that child node altogether, and we’re done.

If the counter doesn’t reach 0, keep decrementing until we reach the end of the word string. Then modify that node to reflect that it is not a word.

Next, let’s implement the delete_words_with_prefix(prefix) function:

def delete_words_with_prefix(self, prefix):
    """
    Delete all words from the trie with the prefix provided.
    :param prefix: Words with this prefix will be deleted.
    :return: None
    """
    count = self.count(prefix)  # Get the count of words with this prefix.
    if count > 0:  # Make sure the prefix actually exists.
        node = self.root

        if self.is_word(prefix):  # If the prefix itself is a word, decrement the root counter by the count.
            node.counter -= count

        for letter in prefix:
            index = self.get_index_of_letter(letter)
            parent = node
            node = parent.children[index]
            node.counter -= count

            if node.counter == 0:  # If the node counter is 0, set the child to None, and we're done.
                parent.children[index] = None

Almost the same logic as the function delete() here. We first get the count of words with the prefix in our trie. If the count is 0, don’t do anything. 

If the counter is greater than 1, then we’ll start by checking if the prefix is a word. If it is, then we’ll decrement the root counter by 1. Then we’ll start iterating through each letter in the string and decrement the counter of each child node by the count we got. When the node’s counter reaches 0, we delete this node from our parent’s children list and we’re done.

Next, let’s implement the is_empty() function:

def is_empty(self) -> bool:
    """
    Returns whether the trie is empty or not.
    :return: Boolean whether trie is empty or not.
    """
    return self.root.counter == 0

We return True if the root counter is 0, False if it is greater than 0.

Next, let’s implement the clear() function:

def clear(self):
    """
    Clears the trie and resets it.
    :return: None
    """
    self.root = TrieNode('*')
    self.root.counter = 0

We reset the root node and set it equal to a new trie node then reset the new node’s counter to 0.

Finally, let’s implement the teach(file) function:

def teach(self, file):
    """
    Adds all words from file provided (assuming it's line-by-line) to trie.
    :param file: File to read to add to trie.
    :return: None
    """
    with open(file) as f:
        for line in f.readlines():
            self.add(line.strip())

This is not really necessary, but this function will basically iterate through a dictionary text file and add each word to the trie. Here’s a link to the one that I’ll use.

Prefix Loop

We’re done with our trie implementation, so let’s test it out by having it return words with a prefix we give it. I implemented a small function called prefix_loop() to test it out.

def prefix_loop(trieObject):
    """
    Function that'll loop and return all possible words from a prefix inputted by user.
    :param trieObject: Trie object to use for searching.
    :return: None
    """
    while True:
        print("Type in a prefix to view all possible words that have it as a prefix. To stop, enter nothing.")
        answer = input(">>").lower()

        if answer == '':
            print("Goodbye.")
            break
        elif not answer.isalpha():
            print("Please make sure you only have alphabet letters.")
        else:
            for suggestion in trieObject.get_words(prefix=answer):
                print(suggestion)
        print()  # Empty print() statement so output looks cleaner.

Test Run

Here’s a test run.

Type in a prefix to view all possible words that have it as a prefix. To stop, enter nothing.
>>apro
apron
aprons
aproape
aprocta
aproctia
aproneer
apronful
aproning
aprotype
aproctous
apronless
apronlike
aprosexia
aprosopia
aprosopous
aproterodont

Type in a prefix to view all possible words that have it as a prefix. To stop, enter nothing.
>>doggi
doggie
doggier
doggies
dogging
doggish
doggiest
doggishly
doggishness